本问题对应的 leetcode 原文链接：剑指 Offer 07. 重建二叉树

问题描述

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1：

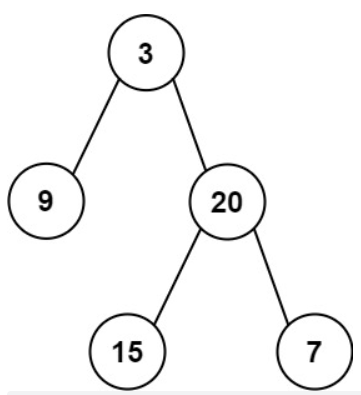
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

解题思路

视频讲解直达： 本题视频讲解

代码实现

    Map< Integer, Integer > map = new HashMap();
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || preorder.length <= 0){
            return null;
        }
        // 简历中序遍历数组的映射（就是为了快速求出某个元素的下标）
        for(int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }

        TreeNode root = f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);

        return root;
    }

    TreeNode f(int[] preorder, int l1, int r1, int[] inorder, int l2, int r2) {
        // 前序遍历或者中序遍历为空时，表示这棵树不存在，直接返回 null
        if( l1 > r1 || l2 > r2){
            return null;
        }
        // 根节点
        TreeNode root = new TreeNode(preorder[l1]);
        // 根节点在中序遍历中的下标
        int i = map.get(preorder[l1]);
        // 递归求解
        root.left = f(preorder, l1 + 1, l1 + (i - l2), inorder, l2, i - 1);
        root.right = f(preorder, l1 + (i - l2) + 1, r1, inorder, i + 1, r2);

        return root;
    }

• 时间复杂度 O(N) ： 其中 NN 为树的节点数量。初始化 HashMap 需遍历 inorder ，占用 O(N) 。递归共建立 NN 个节点，每层递归中的节点建立、搜索操作占用 O(1) ，因此使用 O(N) 时间。
• 空间复杂度 O(N) ： HashMap 使用 O(N) 额外空间；最差情况下（输入二叉树为链表时），递归深度达到 N ，占用 O(N)的栈帧空间；因此总共使用 O(N) 空间。

Python

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def buildTree(self, preorder, inorder):
        """
        :type preorder: List[int]
        :type inorder: List[int]
        :rtype: TreeNode
        """
        map = {}
        for i in range(len(inorder)):
            map[inorder[i]] = i

        def f(preorder, l1, r1, inorder, l2, r2):
            if l1 > r1 or l2 > r2:
                return None
            root = TreeNode(preorder[l1])
            i = map[preorder[l1]]
            root.left = f(preorder, l1 + 1, l1 + i - l2, inorder, l2, i - 1)
            root.right = f(preorder, l1 + i - l2 + 1, r1, inorder, i + 1, r2)
            return root

        return f(preorder, 0, len(preorder) - 1, inorder, 0, len(inorder) - 1)

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        unordered_map<int, int> map;
        for (int i = 0; i < inorder.size(); i++) {
            map[inorder[i]] = i;
        }

        function<TreeNode*(int, int, int, int)> f = [&](int l1, int r1, int l2, int r2) -> TreeNode* {
            if (l1 > r1 || l2 > r2) {
                return nullptr;
            }
            TreeNode* root = new TreeNode(preorder[l1]);
            int i = map[preorder[l1]];
            root->left = f(l1 + 1, l1 + i - l2, l2, i - 1);
            root->right = f(l1 + i - l2 + 1, r1, i + 1, r2);
            return root;
        };

        return f(0, preorder.size() - 1, 0, inorder.size() - 1);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
    m := make(map[int]int)
    for i, v := range inorder {
        m[v] = i
    }

    var f func(int, int, int, int) *TreeNode
    f = func(l1, r1, l2, r2 int) *TreeNode {
        if l1 > r1 || l2 > r2 {
            return nil
        }
        root := &TreeNode{preorder[l1], nil, nil}
        i := m[preorder[l1]]
        root.Left = f(l1+1, l1+i-l2, l2, i-1)
        root.Right = f(l1+i-l2+1, r1, i+1, r2)
        return root
    }

    return f(0, len(preorder)-1, 0, len(inorder)-1)
}

JS

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    const map = new Map();
    if(preorder == null || preorder.length <= 0){
        return null;
    }
    // 建立中序遍历数组的映射（就是为了快速求出某个元素的下标）
    for(let i=0; i<inorder.length; i++) {
        map.set(inorder[i], i);
    }

    let root = f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, map);

    return root;
};

function f(preorder, l1, r1, inorder, l2, r2, map) {
    // 前序遍历或者中序遍历为空时，表示这棵树不存在，直接返回 null
    if( l1 > r1 || l2 > r2){
        return null;
    }
    // 根节点
    let root = new TreeNode(preorder[l1]);
    // 根节点在中序遍历中的下标
    let i = map.get(preorder[l1]);
    // 递归求解
    root.left = f(preorder, l1 + 1, l1 + (i - l2), inorder, l2, i - 1, map);
    root.right = f(preorder, l1 + (i - l2) + 1, r1, inorder, i + 1, r2, map);

    return root;
}

shuaidi永久会员

收藏 海报挣佣金 推广链接